Crtanje pravca koristeći svojstva koeficijenata a i b*
Ako je zadana jednadžba pravca (npr. y = 3/2 x – 1), najjednostavniji način da (koristeći aplet) nacrtamo taj pravac je: upisati jednažbu u polje za unos i stisnuti Enter.
Međutim, ako crtamo na papiru (ili u apletu, ali kao na papiru), onda moramo pronaći (nacrtati) dvije točke koje pripadaju tom pravcu, i kroz njih povući pravac. Prilikom pronalaženja tih dviju točaka, dosad smo morali računati: prvu smo koordinatu uzeli proizvoljnu, uvrstili je u jednadžbu pravca umjesto x i tako dobili drugu koordinatu y (taj smo postupak napravili 2 puta, za svaku točku posebno). Sad ćemo naučiti kako pronaći dvije točke zadanog pravca bez imalo računanja, pomoću odsječka b i nagiba a.
Primjer:
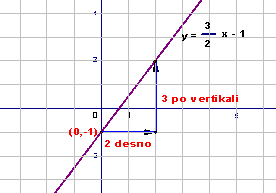
Kako bismo (bez računanja) nacrtali pravac y=3/2 x–1 ?
Postupak (vidi i doljnju sliku):
1. Uočimo koeficijent b, on je u ovom primjeru -1. On nam govori kroz koju točku na osi y prolazi pravac, kroz
(0,-1). Nacrtamo tu točku - time smo dobili jednu točku pravca.
2. Da bismo našli još jednu točku pravca, uočimo koeficijent a! U našem je primjeru a=3/2. On je koeficijent smjera, govori o nagibu pravca, pa nam kazuje i kuda trebamo krenuti od prethodno pronađene točke. Od prethodno nacrtane točke krećemo:
- udesno onoliko “koraka” koliki je nazivnik od a (u ovom primjeru 2 koraka), a zatim:
- gore ako je a>0, a dolje ako je a<0, za onoliko “koraka” koliki je brojnik od a (u ovom primjeru 3 koraka gore). Nacrtamo točku do koje smo tako došli - to je druga točka traženog pravca. Sad kroz te dvije točke nacrtamo pravac. I to je to! J
Sad riješi sljedeći zadatak:
Reset apleta: dugme
Osvježi.
Zoom: desna tipka
miša (u blizini ishodišta).
Zadatak:
Gore opisanim postupkom u apletu nacrtaj zadane pravce (provjeru možeš izvršiti koristeći polje za unos):
a) y = 2/3 x – 2 b) y = -1/4 x – 1 c) y = 2 x + 3 d) y = -x + 2
Za one koji žele znati više:
| 3 Jednadžbe paralelnih pravaca |