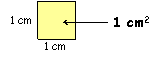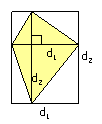Jednostavna objašnjenja nekih formula
za površinu, oplošje i volumen
Autor: Keith Enevoldsen, originalna stranica na engleskom jeziku: http://thinkzone.wlonk.com/Area/AreaVol.htm
Prevela na hrvatski jezik, prilagodila i uz dozvolu autora unijela izmjene: Antonija Horvatek, Matematka na dlanu
Ako zatrebate, na sljedeća dva linka možete naći sistematizirane formule bez objašnjenja i slike geometrijskih tijela .
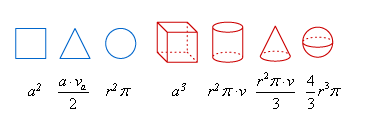
Pamtiš li formule za površinu, oplošje i volumen bez razumijevanja?
Na ovoj stranici možeš naći jednostavna objašnjenja mnogih od njih. Krenut ćemo s jednostavnijim formulama i nastaviti prema složenijima, sve do formula za oplošje i volumen kugle.
Površine geometrijskih likova
Općenito
Površina bilo kojeg lika je veličina njegove unutrašnjosti.
Mjerne jedinice za površinu su: kvadratni metar (m2), kvadratni decimetar (dm2), kvadratni centimetar (cm2) itd.
|
Kvadrat čije su stranice duge 1 cm ima površinu 1 cm2. |
|
|
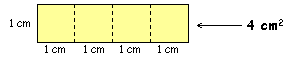
Ako za prekrivanje nekog lika trebamo npr. 4 takva kvadrata, onda je površina tog lika 4 cm2 . |
|
Nadalje:
- kvadrat čije su stranice duge 1 dm ima površinu 1 dm2,
- kvadrat čije su stranice duge 1 m ima površinu 1 m2,
itd.
Četverokuti
1. Pravokutnik
|
|
P = a·b |
Objašnjenje formule: |
||
|
Npr. |
|
P = 5 ·2 = 10 cm2 |
||
|
Općenito: Ako su duljine stranica pravokutnika a i b, tada u 1. redak možemo staviti točno a jediničnih kvadrata, u 2. redak opet a jediničnih kvadrata itd., a bit će točno b redaka. Stoga je ukupan broj jediničnih kvadrata a·b . |
||||
2. Četverokut s okomitim dijagonalama
|
|
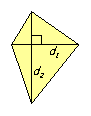
P = 1/2 · d1 · d2 |
Objašnjenje formule:
|
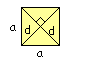
3. Kvadrat
|
|
P = a 2
P = 1/2 · d 2 |
Objašnjenje formula: Druga formula je posljedica činjenice da se dijagonale kvadrata sijeku pod pravim kutom i formule navedene pod 2. Koju formulu koristiti u konkretnom slučaju, ovisi o tome je li nam poznata stranica a ili dijagonala d. Ako nekom kvadratu znamo i duljinu stranice i duljinu dijagonale, svejedno je po kojoj ćemo formuli računati - u oba slučaja dobivamo isti rezultat. |
4. Paralelogram
|
|
P = a · va |
Objašnjenje formule:
|
5. Romb
|
|
P = a · va
P = 1/2 · d1 · d2 |
Objašnjenje formula:
Koju formulu koristiti u konkretnom slučaju, ovisi o tome je li nam poznata stranica a ili dijagonale d1 i d2 . Ako nekom rombu znamo i duljine stranica i duljine dijagonala, svejedno je po kojoj ćemo formuli računati - u oba slučaja dobivamo isti rezultat. |
6. Trapez
|
|
P = 1/2 · (a + c) · v |
Objašnjenje formule:
|
|
|
|
Površina paralelograma na slici: P = (a+c) · v |
||
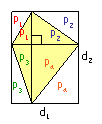
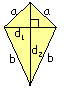
7. Deltoid
|
|
P = 1/2 · d1 · d2 |
Objašnjenje formule: |
Trokuti
8. Trokut - općenito
|
|
P = 1/2 · a · va |
Objašnjenje formule:
|
9. Pravokutni trokut
|
|
P = 1/2 · a · b i P = 1/2 · c · vc
|
Objašnjenje formula: Drugu formulu dobivamo primjenom formule P=1/2·a·va na stranicu c. |
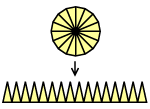
Krug
|
|
P = r2 π |
Objašnjenje: 1/2 puta zbroj njihovih donjih stranica (a one su zajedno duge kao cijela kružnica, tj. 2rπ) puta visina tih trokuta (a to je r).
|
Oplošja i volumeni geometrijskih tijela
Općenito
Oplošje tijela je zbroj površina svih likova koji omeđuju to tijelo.
To je površina materijala (npr. kartona, papira...) kojeg bismo upotrijebili pri izradi tog tijela.
Mjerne jedinice za oplošje su iste kao i za površinu, dakle m2, dm2, cm2...
Volumen (obujam) tijela je veličina unutrašnjosti tijela.
To je količina npr. pijeska, vode i sl. koje bismo trebali da bismo popunili unutrašnjost tijela.
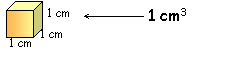
Mjerne jedinice za volumen su: kubični metar (m3), kubični decimetar (dm3), kubični centimetar (cm3) itd.
|
Kocka čiji su bridovi dugi 1 cm ima volumen 1 cm3. |
|
|
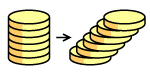
Ako za popunjavanje nekog tijela trebamo npr. 3 takve kocke, onda je volumen tog tijela 3 cm3 . |
|
Nadalje:
- kocka čiji su bridovi dugi 1 dm ima volumen 1 dm3,
- kocka čiji su bridovi dugi 1 m ima volumen 1 m3,
itd.
Osim kubičnih mjernih jedinica, volumen možemo mjeriti i u litrama (l ), decilitrima (dl ) itd.
Veza između tih dviju vrsta mjernih jedinica je: 1 dm3 = 1 l .
Prizma i valjak
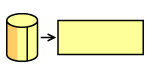
1. Površina plašta valjka čiji je polumjer baze r a visina v je P=2rπv .
|
|
Objašnjenje: |
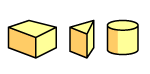
2. Volumen prizme i valjka, bilo uspravnih ili kosih, s bazom površine B i visinom v je V=Bv. Posebno, volumen kvadra je V=abc, volumen kocke V=a3, a volumen valjka V=r2πv .
|
|
Objašnjenje glavne formule
V=Bv za uspravnu prizmu
i uspravni valjak: Naime, pitamo se s koliko jediničnih kocki možemo popuniti zadanu prizmu ili valjak. Budući da površina baze B (po definiciji pojma površine) govori koliko je jedničnih kvadrata potrebno za popunjavanje baze, onda isti taj broj B govori i koliko je jedinčnih kocki potrebno za prekrivanje baze. Dakle, prilikom popunjavanja prizme/valjka, u 1. sloj stane točno B jediničnih kocki, no tada i u 2. sloj stane također B jedničnih kocki (slažemo kocku na kocku) itd., a ukupno ima v slojeva. Stoga je tu ukupno B·v jediničnih kocki, pa je V=Bv.
Objašnjenje formula za kvadar, kocku i valjak, V=avc, V=a3,
V=r2πv
: |
Piramida i stožac
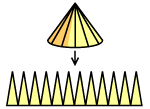
3. Površina plašta uspravnog stošca čiji je radijus baze r a duljina izvodnice s je P=rπs.
|
|
Objašnjenje: 1/2 puta zbroj njihovih donjih stranica (a to je jednako opsegu baze 2rπ) puta visina tih trokuta s. |
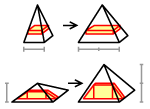
4. Volumen piramide (bilo uspravne ili kose) s površinom baze B i visinom v je V=Bv/3.
|
Objašnjenje u 3 koraka: | |
|
|
1. korak: Volumen piramide je proporcionalan površini baze B, a ujedno i visini v . Naime, zamislimo da se udvostruči baza ili visina. Udvostručenje baze će uzrokovati udvostručenje volumena po svakom vodoravnom presjeku. Udvostručenje visine uzrokovat će udvostručenje volumena po svakom uspravnom presjeku.
|
|
|
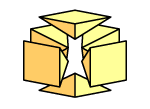
2. korak: Konstanta proporcionalnosti mora biti 1/3. Naime, ako krenemo od piramide čija je baza kvadrat 1x1, a visina 1/2, i ako 6 takvih piramida spojimo kao što prikazuje slika, one će zajedno činiti kocku 1x1x1, a njezin je volumen 1. Stoga je volumen polazne piramide jednak 1/6, a to je 1/3·B·v . |
|
|
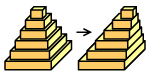
3. korak: Kosa piramida ima isti volumen kao i uspravna piramida s istom bazom i visinom. Naime, krenimo od uspravne piramide, zamislimo da je ona podijeljena na puuuno tankih vodoravnih slojeva, te pomaknemo te slojeve da bismo dobili kosu piramidu. Pomakom slojeva volumen se nije promijenio.
|
5. Volumen stošca (bilo uspravnog ili kosog) s polumjerom baze r i visinom v je V=r2πv/3.
|
|
Objašnjenje: Kosi stožac ima istu formulu. Objašnjenje je isto kao i (gore) za kosu piramidu. |
Kugla
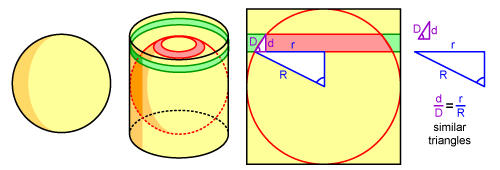
6. Oplošje kugle polumjera r je O=4r2π.
|
|
|
Objašnjenje: Uočimo da je površina plašta
valjka koji ima polumjer baze r i visinu 2r
upravo P=2rπv = 2rπ·2r
= 4r2π . |
7. Volumen kugle je V=4/3 ·r3π .
|
|
Objašnjenje : 1/3 puta površina baze piramide puta visina piramide (a visina piramide je polumjer kugle r), a nakon zbrajanja svih tih volumena dobivamo umnožak: 1/3 puta površina cijele sfere (a to je 4r2π ) puta polumjer kugle r . Otuda slijedi V=4/3·r3π . |
Povijesna napomena: Prva osoba koja je otkrila kako se računaju oplošje i volumen kugle bio je Arhimed.
PDF format na engleskom jeziku

PDF |
Uvjeti korištenja |
Kupite poster
Autor: Keith Enevoldsen
Originalna stranica na engleskom jeziku: http://thinkzone.wlonk.com/Area/AreaVol.htm
Home stranica: Keith Enevoldsen's Think Zone
Prevela na hrvatski jezik, prilagodila i uz dozvolu autora unijela izmjene: Antonija Horvatek
Ova je stranica dio weba:
Matematka na dlanu
Najtoplije zahvaljujem autoru na dopuštenju da stranicu prevedem na hrvatski jezik, unesem promjene i objavim u sklopu svojih web stranica.
Antonija Horvatek